数学家列昂纳多·斐波那契研究了野外兔子的繁殖问题:一般而言,兔子出生两个月后,就有繁殖能力。假设一对兔子每个月能生出一对小兔子而且所有兔子都不死。如果现在往一片没有兔子的新大陆上放生一对新生的兔子,那么一年以后那个大陆上有多少只兔子?两年以后呢?
版权声明
本文可以在互联网上自由转载,但必须:注明出处(作者:海洋饼干叔叔)并包含指向本页面的链接。
本文不可以以纸质出版为目的进行改编、摘抄。
第1个月,那对兔子还没有繁殖能力,仍为幼兔。故幼免数量为1对,成兔数量为0对,总对数为1;
第2个月,那对兔子性成熟,变成成兔。故幼兔数量为0对,成兔数量为1对,总对数为1;
第3个月,2月时的成兔1对,生了1对小兔子,故幼兔1对,成兔1对,总对数为2;
第4个月,3月时的成兔1对生了1对小兔子,且3月时的幼兔1对变成了成兔,故幼兔数量为1对,成兔变成了2对,总对数为3…
| 经过月数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幼仔对数 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
| 成兔对数 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 |
| 总对数 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 |
简单归纳,容易导出下述结论:
幼免对数 = 前月成兔对数 (每对成兔每月生一对小兔子)
成兔对数 = 前月成兔对数 (成兔不死) + 前月幼兔对数(前月的幼兔长大变成成兔)
总对数 = 幼兔对数 + 成兔对数
观察上述表格,可以发现,上述三行数据,在1,1后的每一个数字,都正好等于前两个数字之和。2 = 1 + 1, 3 = 1+2, 5 = 2 + 3… 89 = 34 + 55…
斐波那契对上述规律进行总结和形式化,得到关于n个月后兔子数量的通项公式如下,这是一个分段函数。
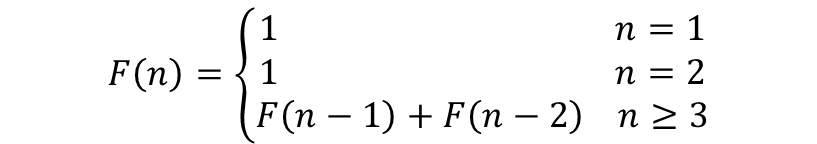
读者希望知道10年,也就是120个月之后的兔子数量吗? 我们来计算一下。
1 | [fib1.py] |
执行结果:
1 | month: 1 rabbits: 1 |
函数fibonacci(n)计算并返回第n个月后的免子对数。计算结果几乎是反直觉的。如果这块新大陆无限大,食物无限丰富,而且没有灰太狼,那么120个月以后,兔子的总对数为:5358359254990966640871840。恭喜成都的朋友们,他们拥有了”永远”也啃不完的麻辣兔头。
上述fibonacci函数值随参数的增长速度极其惊人。在计算复杂性问题上,研究函数的值随参数的增长速度,是有一件有趣的事情。接下来,我们比较一下下述函数以及斐波那契函数随参数的增长速度:
$$
y = n^2\y = n^3
$$
1 | #grow.py |
执行结果:
1 | n^2= [1, 4, 9, 16, 25, 36, 49, 64, 81, 100] |
上述代码首先生成了一个x列表,其值为[1,2,3,4,5,6,7,8,9,10];然后对x列表每一个值,逐一计算其平方,立方及斐波那契函数的值。最后使用matplotlib将四个函数绘制出来。matplotlib是一个绘图用的扩展模块,需要通过在命令行中执行pip install matplotlib进行安装。
下图展示了参数取值1-10时,3个函数的增长曲线图:
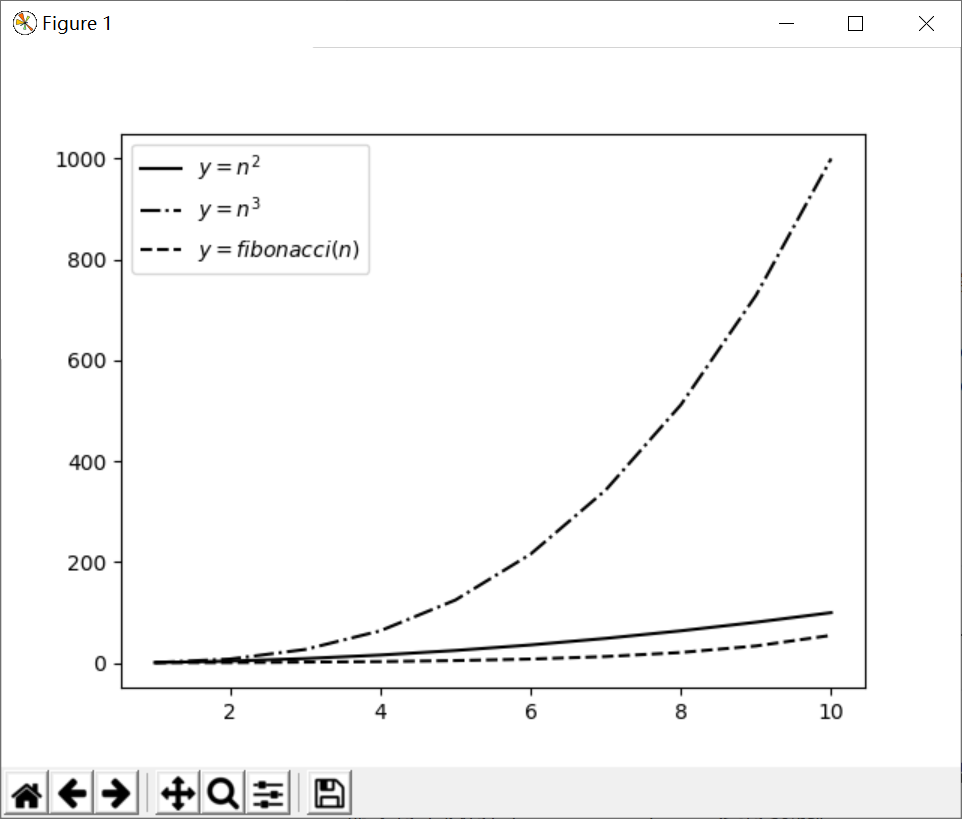
看起来,n3增长较快,n2和fibonacci(n)增长较慢。这不是事实! 我们把参数取值范围扩大到1-30,重新绘图,结果如下:
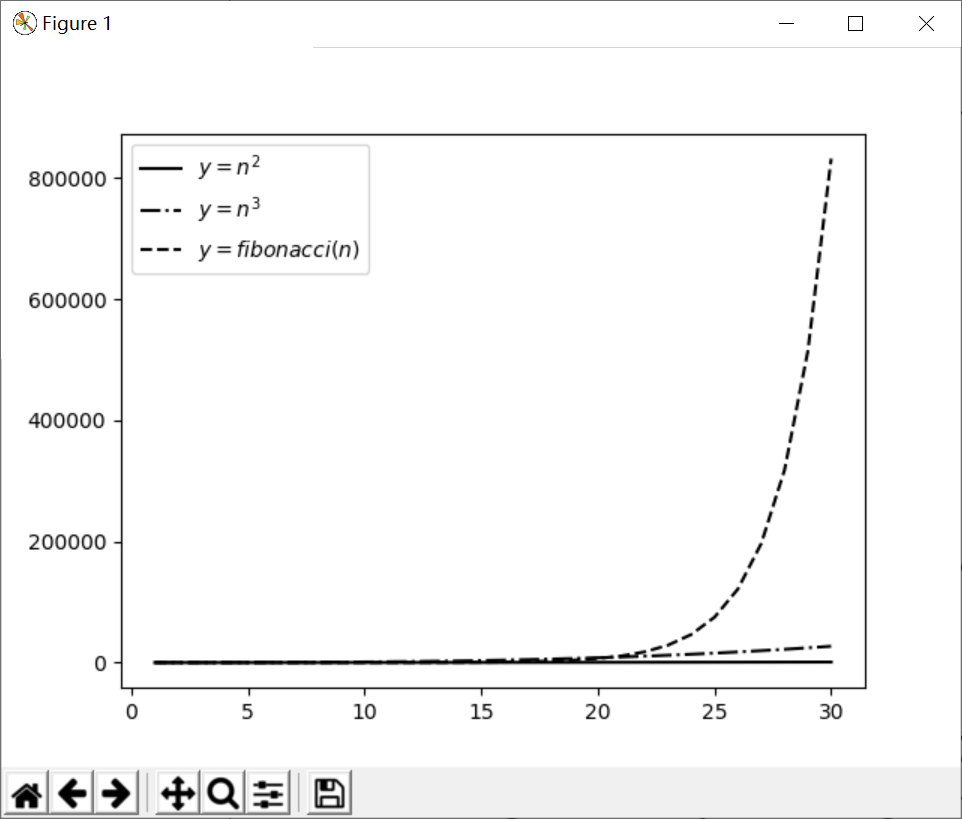
可以看到,斐波那契函数的增长曲线昂首挺胸,而n2以及n3在该尺度下,几乎趴在了地上。读者可以自行试验一下x取值1-100的情况。
相对于斐波那契函数,n3的增长速度实在是太慢了。从数学上讲,斐波那契函数与n3都是n趋近于无穷大时的无穷大,但显而易见,斐波那契函数拥有更高的阶。
本文内容节选自作者编著的《Python编程基础及应用》(高等教育出版社)一书。

免费随书B站MOOC:




