据说蝴蝶扇动翅膀这样一件小事,可能最终会引起对面半球的一场飓风。
— 混沌理论
上面这行话来源于2004年的电影《蝴蝶效应》的开篇字幕。更早期,这段话则与气象学家Edward Lorenz有关。他发现简单的热对流现象居然能引起令人无法想象的气象变化,在对相关发现进行数学分析后,Lorenz于1963年提出了混沌理论 - Chaos Theory。混沌理论认为在混沌系统中,初始条件十分微小的变化,经过不断放大,对其未来状态会造成极其巨大的差别。
经过多年的发展,该理论已在气象、经济、化学、信息等诸领域得到广泛应用。但如果以混沌理论为关键词在Google上进行搜索,还会发现一些美轮美奂的艺术作品,这些艺术作品都与混沌理论中的吸引子有关。
版权声明
本文可以在互联网上自由转载,但必须:注明出处(作者:海洋饼干叔叔)并包含指向本页面的链接。
本文不可以以纸质出版为目的进行改编、摘抄。
1. Peter de Jong吸引子
所谓吸引子 - Attractor,是动力系统里的一个状态,系统演化会趋向那个方向靠拢。Peter de Jong是一个奇异吸引子。奇异吸引子上的运动对初始值表现出极强的敏感依赖性,在初始值上的微不足道的差异,就会导致运动轨道的截然不同。奇异吸引子往往具有非整数维,如2.06维、1.2365维等。
Peter de Jong吸引子就是一个奇异吸引子,它可以由下述迭代方程描述:
$$
x_{n+1} = sin(ay_{n})-cos(bx_{n})\
y_{n+1} = sin(cx_{n})-cos(dy_{n})
$$
这个方程有4个参数,分别为a,b,c,d。随意指定x0和y0的值,比如(0,0),通过上述公式,可计算得x1和y1。然后以x1和y1为基础,可计算得x2,y2 …… 这样一直迭代-iterate计算,我们就可以获得N个平面上的点(xi,yi),把这些点在坐标系中画出来,就得到Peter de Jong吸引子的图像。
1 | #SimplePeterDeJong.py |
程序只有寥寥数行。首先我们从math模块导入了正弦-sin和余弦-cos函数;还导入了matplotlib中的pyplot模块并取名为plt。matplotlib是著名的C/C++语言编写的绘图包,可以很简单地生成各种图表。
iteration()函数进行迭代计算,首先初始化x = 0, y = 0,然后迭代计算100万个点,并把相应数据存入xdata,ydata列表并返回。xdata,ydata列表中存储了100万个点,其中第i个点的x轴坐标数据为xdata[i],y轴坐标数据为ydata[i]。
plt.figure(figsize=(6,6))创建了一个长6英寸,宽6英寸的图-Figure,plt.title()函数设置了图的标题,plt.scatter()函数则在xy平面上绘制散点图,相应点的坐标数据包含在xdata及ydata列表中,s参数指定了点的绘制尺寸。plt.show()则把绘制好的图显示在屏幕上。程序运行结果如下:
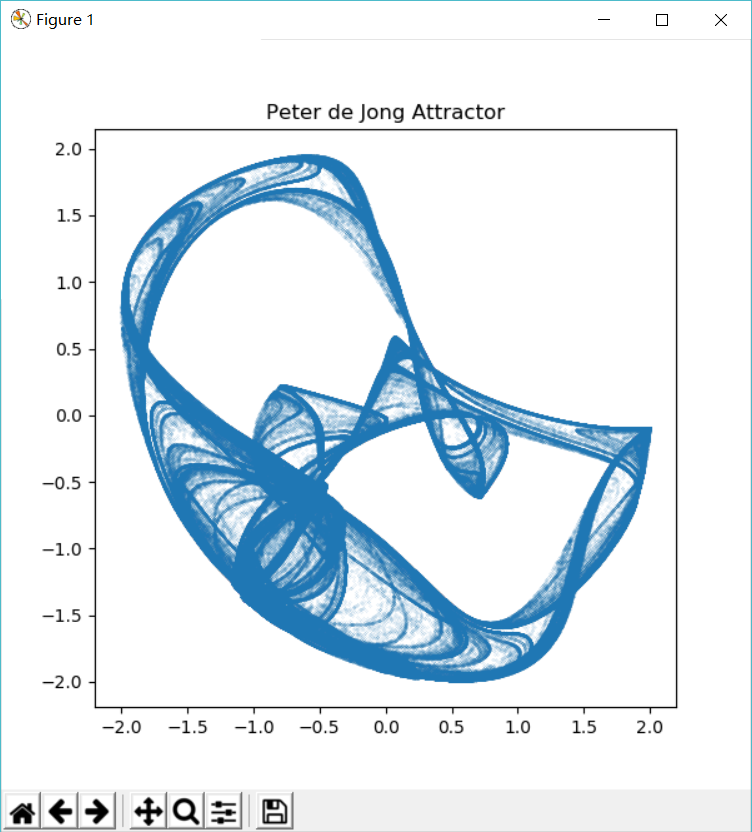
在上图中,可以看到,x,y坐标的取值范围都是[-2, +2]。这是因为正弦函数和余弦函数的值域都是[-1, +1],上述x,y取值为一个sin()减去一个cos(),两者各取极值,可得[-2,+2]的值域。
这个图表示了Peter de Jong吸引子的点的分布。它表现出混沌特性,当a,b,c,d的参数值不同时,图像差异会很大。为了把图变得美观一点,我们引入颜色。
2. 彩色PDJ吸引子
1 | #ColoredPeterDeJong.py |
这段代码同前述代码有以下区别。首先,我们引用了新的参数e,f,并引入了z值。该z值以类似于x,y的方式被迭代计算,并通过zdata列表返回。
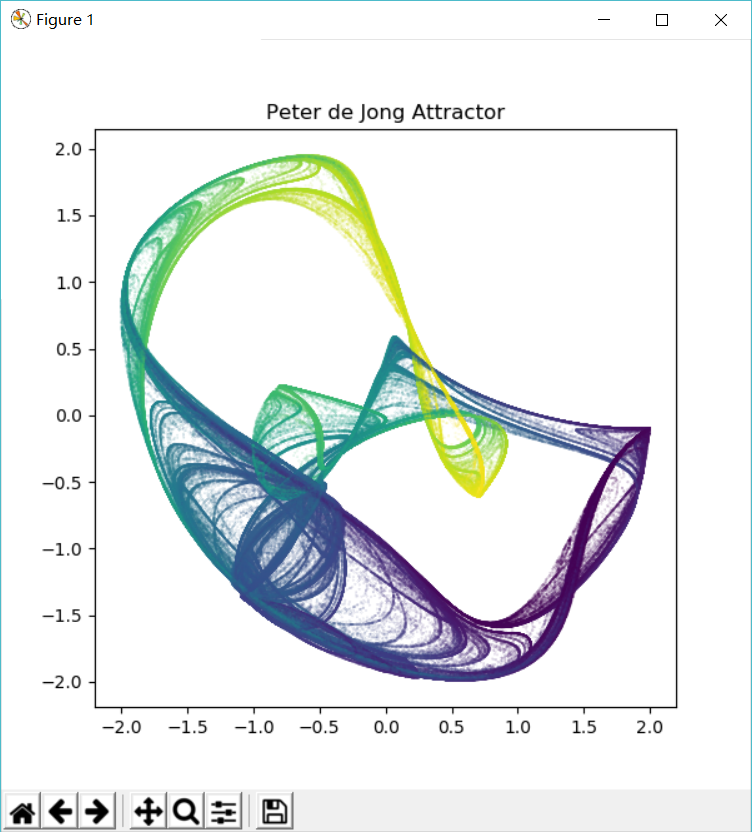
在plt.scatter()函数中,c=zdata表示每个散点的颜色从zdata列表中获取,即第i个散点的颜色数据为zdata[i]。至于matplotlib如何把zdata当中的浮点数据转换成实际的颜色,在这里作者没有深入探究。新程序的执行结果如下图。
3. 修改PDJ参数
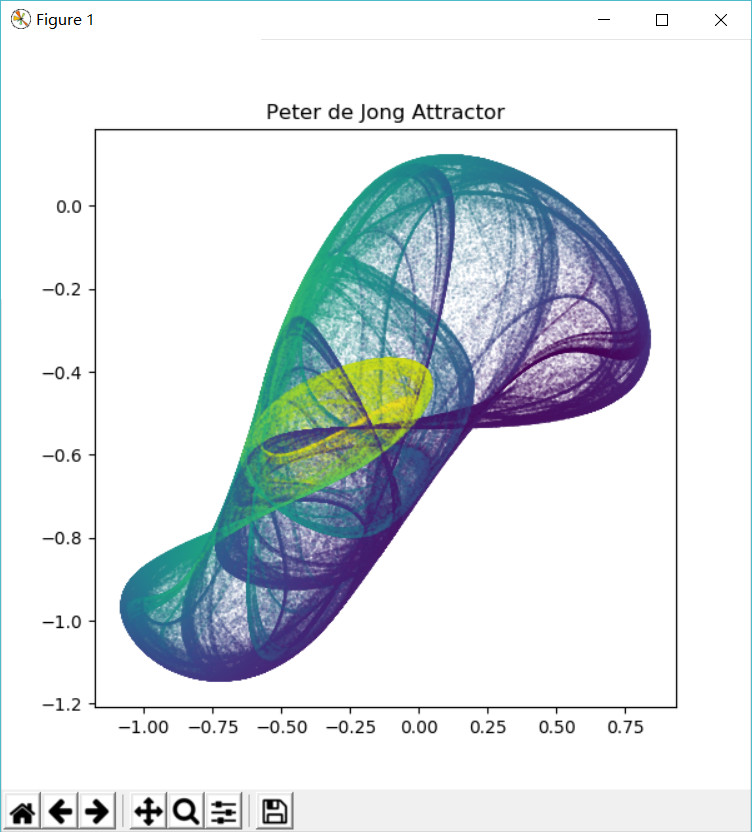
作者尝试了几个不同的a,b,c,d参数,得到下述吸引子图像。
 |
 |
|---|---|
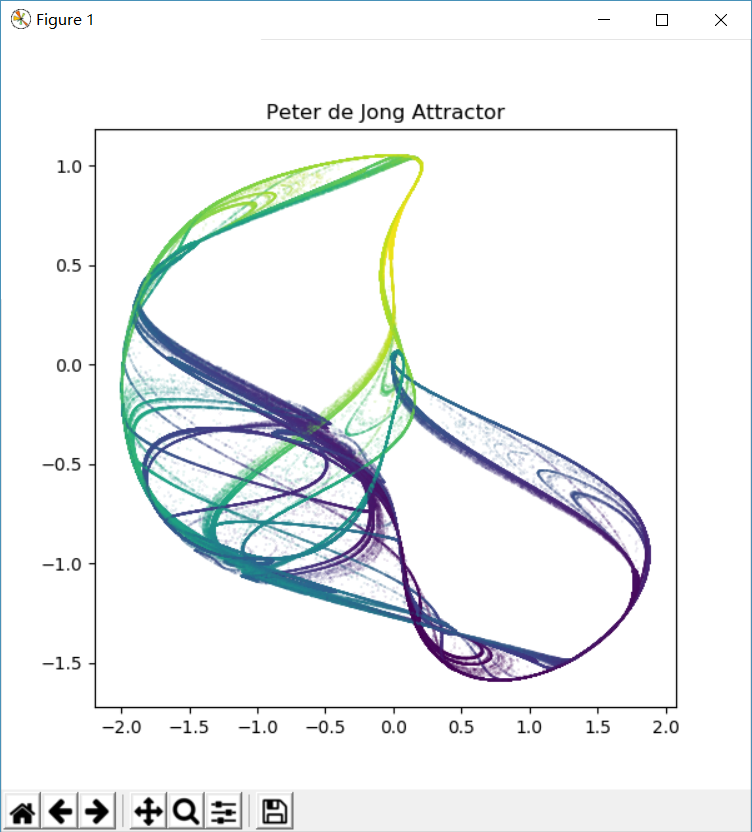
| a,b,c,d = -0.709,1.638,0.452,1.740 | a,b,c,d = 1.641,1.902,0.316,1.525 |
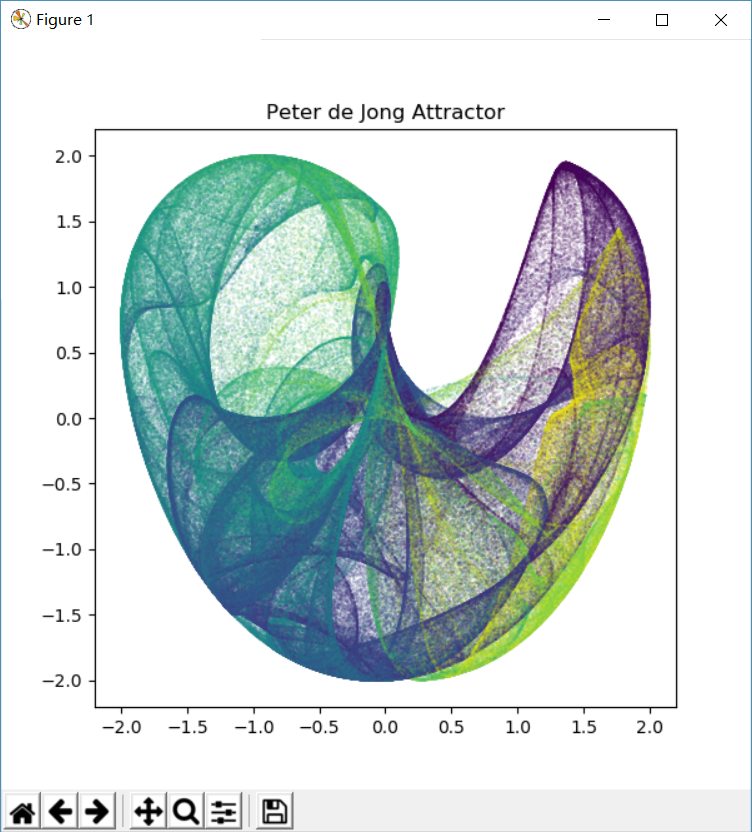 |
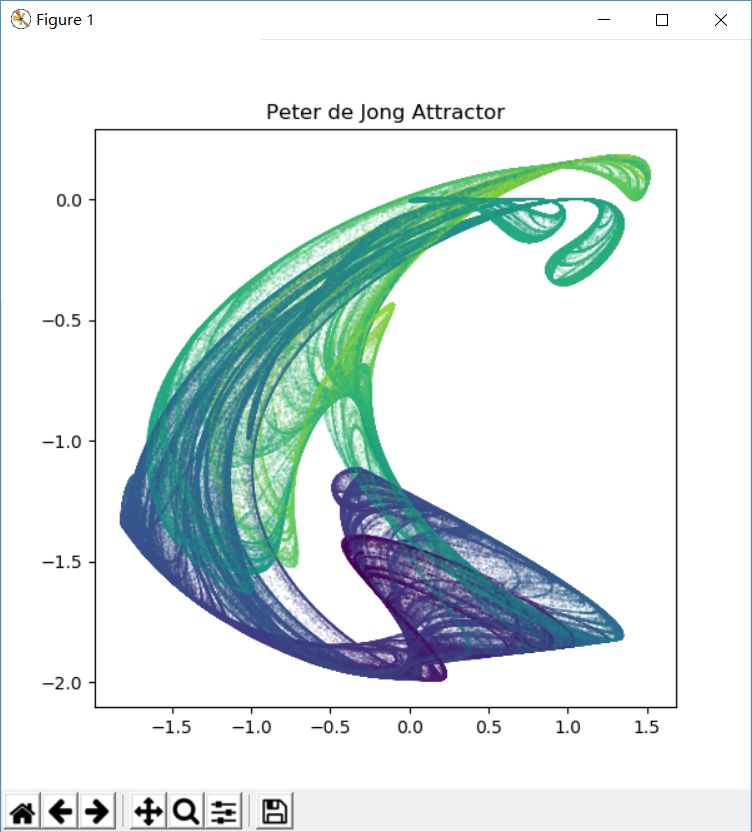 |
| a,b,c,d = 1.4,-2.3,2.4,-2.1 | a,b,c,d = 2.01,-2.53,1.61,-0.33 |
严格地说,上述吸引子图像远没有达到“艺术”效果。要想把上述吸引子图像画成“艺术”效果,需要图像渲染算法的知识,在这里没办法展开。其中一种比较有名的算法称之为分形火焰算法 - fractal flame algorithm。
本文内容节选自作者编著的《Python编程基础及应用》(高等教育出版社)一书。

免费随书B站MOOC:




