汉诺塔递归算法/搬金盘的婆罗门 - Python实现

汉诺塔递归算法/搬金盘的婆罗门 - Python实现

版权声明

本文节选自作者本人的图书《Python编程基础及应用》，高等教育出版社。本文可以在互联网上自由转载，但必须：注明出处(作者：海洋饼干叔叔)并包含指向本页面的链接。本文不可以以纸质出版为目的进行改编、摘抄。本书同名免费MOOC《Python编程基础及应用》在哔哩哔哩（B站）热播，作者带着你学。

17.1 汉诺塔问题

法国数学家爱德华·卢卡斯曾转述过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根金刚石柱。印度教的主神梵天在创造世界的时候，在其中一根石柱上从下到上的穿好了由大到小的64块金盘，这就是所谓的汉诺塔 - Hanoi Tower。

按照梵天的命令，不论白天黑夜，总有一个婆罗门僧侣在按照下面的规则移动这些金盘：一次只移动一个盘，不管在哪根柱上，小盘必须在大盘上面。僧侣们预言，当所有的金盘都从梵天穿好的那根柱上移到另外一根柱上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

​

17.1.1 求解

如下图所示的5个盘的汉诺塔问题，其总任务是将A柱上的n = 5个盘移至C柱。要实现这个总任务并且保证移盘过程中小盘始终在大盘上面，整个过程分三步实现。第1步：我们必须先将n - 1 = 4个黑盘从A柱移至B柱。在第1步的执行过程当中，为了保证规则的贯彻，显然，必须借助于C柱作为中转柱才能完成。

第1步所做的工作可描述为：借助中转柱C， 将n-1=4个盘从A移至B。

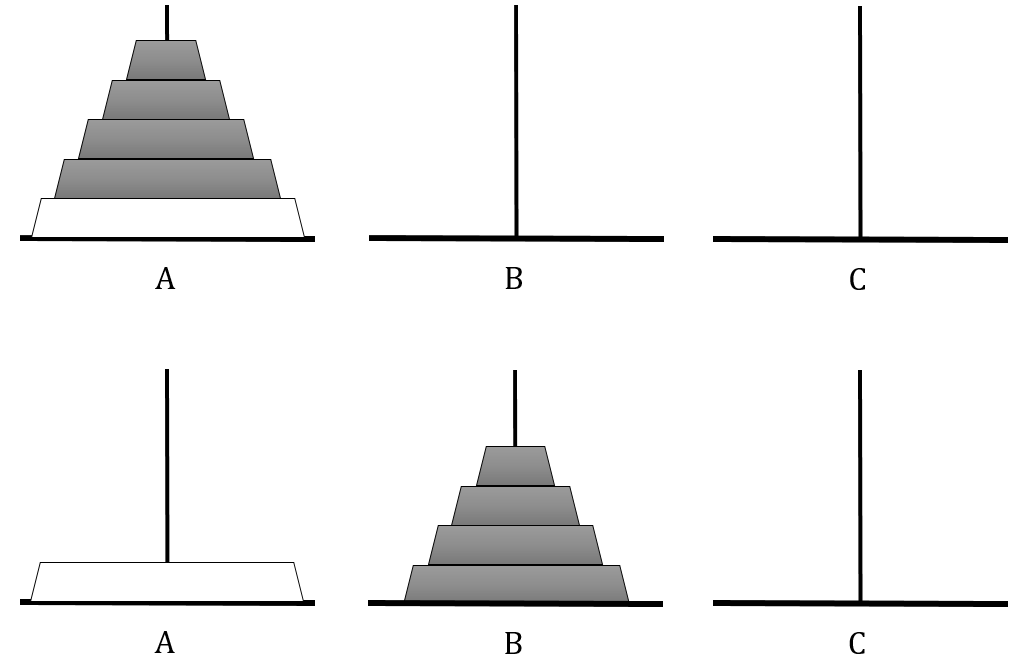
​ 现在，最大的白盘在A柱上，C柱是空的。可实施第2步：将A柱上的大盘取下，移至C柱。

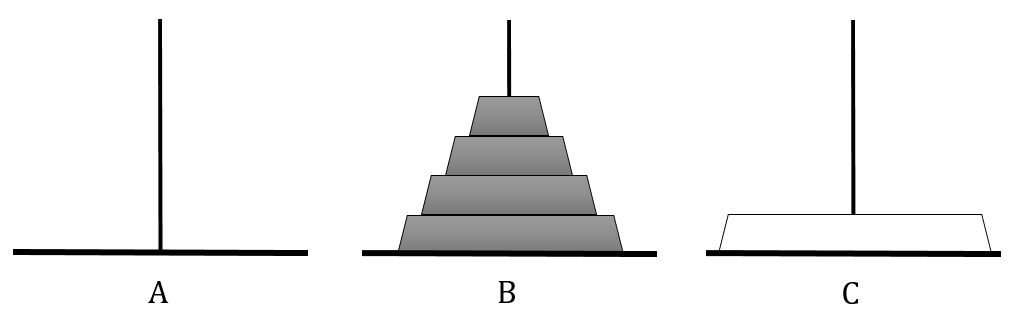
接下来，我们要做的是第3步: 借助中转柱A，将B柱上的n - 1 = 4个盘移至C柱。此时，C柱上虽然已经有了一个盘，但由于此盘是最大的，所以只要移动过程中不搬动C柱上的原有大盘，可以忽略其存在。

​

现在，我们试图总结一下总任务及其三个子任务：

不难看出，除了柱子不同，子任务3同子任务1所做的工作是一样的，都是把 n - 1 个盘从一个柱移至另一个柱。同时，子任务1，3与总任务之间也极其相似，除了需要移动的盘子数量差异外。

我们称，将n - 1个盘子从A移至B的汉诺塔问题，与原问题 - 即“将n个盘子从A移至C的汉诺塔问题”的性质完全相同，区别仅在于问题的规模 - 需要移动的盘子数量稍小。我也称为前者是原问题的子问题。

如果我们能将n - 1 = 4个盘子从A移至B，从B移至Ｃ，那么n = 5个盘子的汉诺塔问题可解。那么如何求解4个盘子的汉诺塔问题呢？ 聪明的读者已经有了答案。

​ 下面的图展示了这一过程：

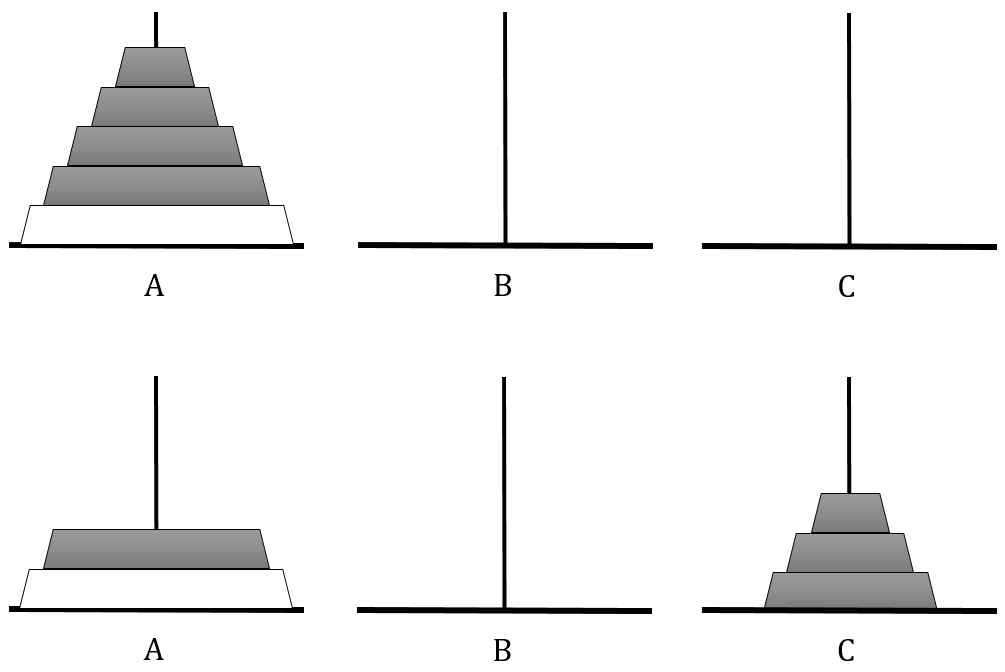
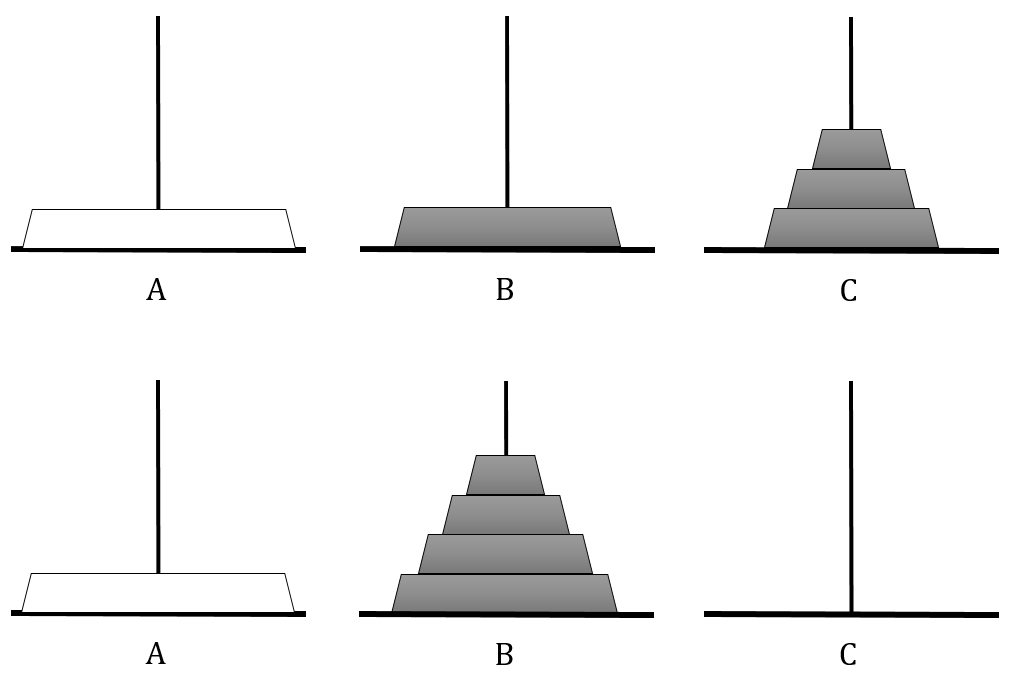
上面的分析可以看出，5盘汉诺塔问题可以通过求解4盘汉诺塔问题来解决，4盘汉诺塔问题可以通过求解3盘汉诺塔问题来解决。同理，3盘汉诺塔问题可以通过求解2盘汉诺塔问题来解决，2盘汉诺塔问题可以通过求解一盘汉诺塔问题来解决。而一盘汉诺塔问题，由于问题的规模足够小，可直接解决：把盘从原柱搬至目标柱即可。所以在前表中，我们称其为“简单任务”。

17.1.2 递归算法

根据前一小节描述的算法思想，我们可以写出汉诺塔问题求解的递归算法。

1
2
3
4
5
6
7
8
9
10
11
12
13

#BasicHanoi.py
def hanoi(n, a, b, c):
    if n == 1:
        movements.append(a + " --> " + c)
    else:
        hanoi(n - 1, a, c, b)
        movements.append(a + " --> " + c)
        hanoi(n - 1, b, a, c)

movements = []
hanoi(5, 'A', 'B', 'C')
print("Steps count:",len(movements))
print("The first 3 steps are:", movements[:3])

函数hanoi(n,a,b,c)用于生成以b为中转柱，将n个金盘从a移至c的移盘序列。可以看到，这个递归函数的执行过程跟前节的总任务-子任务分解完全一致。当n == 1时，只有一个盘子，简单任务，直接移盘。如果n > 1，则分解为两个 n - 1 的汉诺塔子问题，以及一个简单移盘任务。子问题的求解以函数递归调用来解决。

上述代码的执行结果如下：

1
2

Steps count: 31
The first 3 steps are: ['A --> C', 'A --> B', 'C --> B']

上述结果表明，5盘汉诺塔问题共需要31次移盘。movements列表中按顺序存储了全部的移盘动作。

17.1.3 计算复杂性

使用前小节中的程序，作者尝试计算了n = 5 … 12汉诺塔问题的移盘过程，得到下述移盘次数。

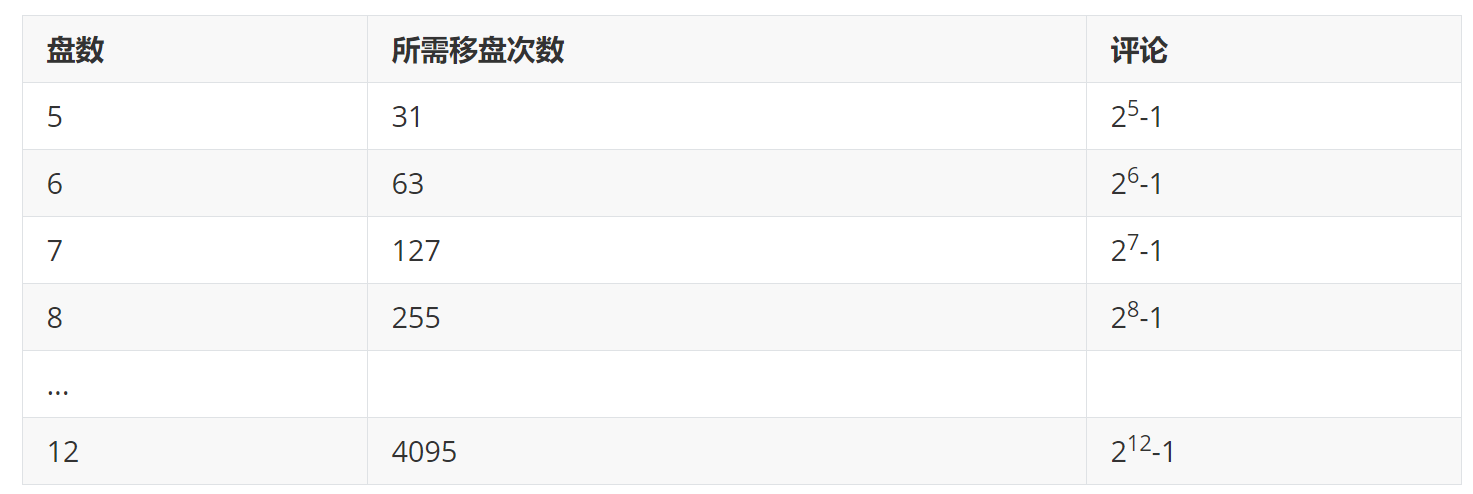
看起来，似乎n个盘的汉诺塔问题的移盘次数为2ⁿ-1。事实上，对移盘次数的数学分析可以证明这个结论。n盘的汉诺塔求解可以拆分成两个n-1盘的汉诺塔求解再加上1次简单移盘。如果用T(n)来表示n盘汉诺塔的移盘次数的话，函数T(n)可使用下述递归定义。

​

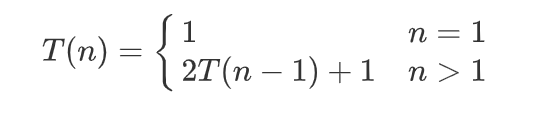
我们试着把递归函数消解成非递归函数。

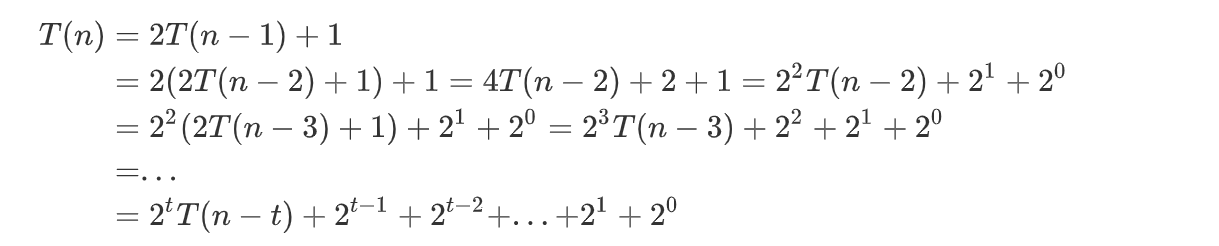
令t = n - 1，有：

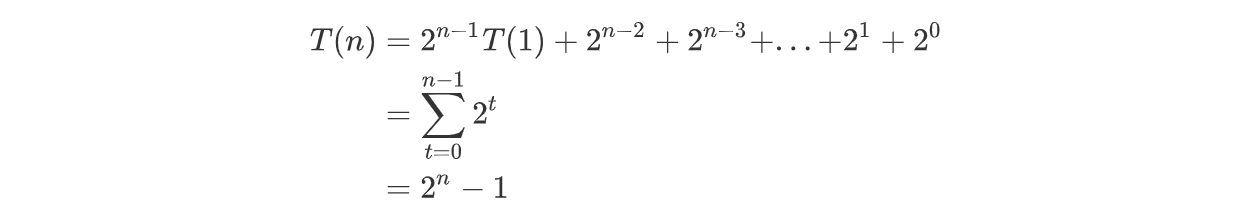
故n盘汉诺塔共需移盘2ⁿ-1次。那么，如果梵天规定的是64个金盘的话，总移动次数则为2⁶⁴-1 = 18446744073709551615。如果婆罗门僧侣是个熟练工，1秒挪一个盘，那么1小时可以移3600个盘，1年可移3600 x 24 x 365 = 31536000个盘(忽略闰年误差）。那么，解64盘汉诺塔问题共需要(2⁶⁴-1)/31536000年，即大约5949亿年。看起来，按照当前的人类知识，印度的古老智慧好像高估了地球的预期寿命。

读者不要去尝试计算hanoi(64,’A’,’B’,’C’)，显然，在你有限的人生里，是无法完成这件接近“无限”的大事的。而且，因为递归所导致的内存消耗，你有限的计算机内存也排除了这种可能性。

作者是无神论者，上述探讨基于严谨的数学，作者不相信任何人格化的“上帝 ”。

本书同名免费MOOC《Python编程基础及应用》在哔哩哔哩（B站）热播，点击加入，作者带着你学。