数学的美可以用Python证明 ——分享与数学有关的几个有意思的程序设计教学案例

海洋饼干叔叔

发布于：2019年11月7日

Python

高数差不多是大多数莘莘学子共同的噩梦。

“ 从前有棵树，叫高数，树上挂了很多人。透过浓密的树叶向上看，拉格朗日挂在天空，向下看，分别是常微分和偏微分两座方城。城里有解析几河，微分几何、黎曼几何几条大河，而作为河的支流的几条小溪，也非常有名，它们是柯溪，数学分溪，回归分溪，泛涵分溪和时间序列分溪。城的外面，有一片树林，树林里有很多树，分别是高等代树、线性代树、数值代树，以及实变和复变函树两兄弟。“

在数学家眼里，数学美得不可方物，她美在简洁、美在奇妙、美在统一、美在严谨。普通如我等凡夫俗子，很难从数学家的高度去欣赏数学的美。好在，我们还有计算机，通过编程，我们可以将一些美妙的数学公式可视化，变幻出五光十色。

[本文中的示例引自《Python编程基础及应用》一书。]

Case 1 - 分形蕨叶

数学名词：分形数学、线性方程组、矩阵乘法

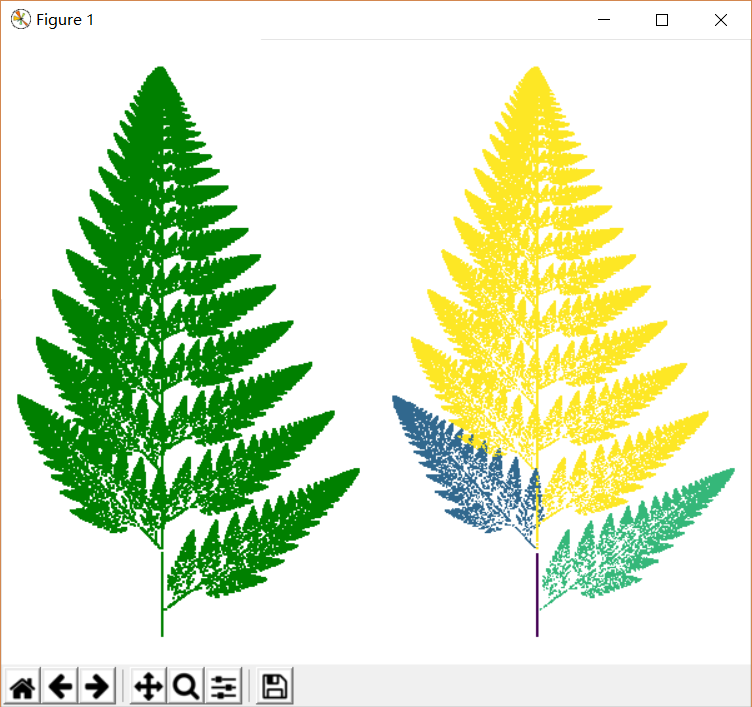
1545843511101

工作原理：这两片树叶并不是普通的二维图像，它是由迭代函数系统（iterated function system）从原始坐标x=0, y=0返复迭代计算出来的。更具体一点，该迭代函数系统包括下述四组线性函数，每组线性函数的选择概率依次是0.01, 0.07，0.07和0.85。系统从坐标点(0,0)出发，随机选择下述线性函数中的一组，即可以得到一个新的坐标点。上述过程重复10万次，即得平面上的10万个点，将所得的全部点以散点图形式画出，即得上述蕨叶图像。
$$
\begin{align}
(1)\space
x_{i+1}&=0\newline
y_{i+1}&=0.15 y_i
\end{align}
$$
$$
\begin{align}
(2)\space
x_{i+1}&=0.21x_{i}-0.19y_{i}\newline
y_{i+1}&=0.24x_{i}+0.27y_{i}+1.5
\end{align}
$$

$$
\begin{align}
(3)\space
x_{i+1}&=-0.14x_{i}+0.26y_{i}\newline
y_{i+1}&=0.26x_{i}+0.25y_{i}+0.47
\end{align}
$$

$$
\begin{align}
(4)\space
x_{i+1}&=0.87x_{i}\newline
y_{i+1}&=-0.05x_{i}+0.84y_{i}+1.54
\end{align}
$$

实例代码：示例代码只有30多行（包括诸多空行在内），蕨叶就像是凭空变出来的一样，Amazing!

#IfsLeaf.py
import numpy as np
from matplotlib import pyplot as plt

def ifs(p,eq,n):
    p = np.cumsum(p)							#对概率列表进行累加运算
    rands = np.random.rand(n)					#生成n个值域为[0,1)的随机数
    select = np.searchsorted(p,rands)			#生成方程组选择数组

    result = np.zeros((n,2),dtype=np.float)		#n行2列的结果数组，元素值初始化为0
    c = np.zeros(n,dtype=np.float)				#n个0值构成的c数组，用于表示点的颜色

    #值为[0,0,1]的当前点坐标数据，可以视为3行1列的矩阵
    pos = np.array([0,0,1],dtype=np.float)		
    for i in range(n):
        eqidx = select[i]
        tmp = np.dot(eq[eqidx],pos)
        pos[:2] = tmp
        result[i] = tmp
        c[i] = eqidx

    return result[:,0],result[:,1],c

#方程组参数矩阵
equations = [np.array([[0,0,0],[0,0.15,0]]),
             np.array([[0.21, -0.19, 0], [0.24, 0.27, 1.5]]),
             np.array([[-0.14, 0.26, 0], [0.26, 0.25, 0.47]]),
             np.array([[0.87, 0, 0], [-0.05, 0.84, 1.54]])]

x,y,c = ifs([0.01,0.07,0.07,0.85],equations,100000)
fig,axes = plt.subplots(1,2,figsize=(6,5))     #生成一行2列两个子图，返回图及子图列表
axes[0].scatter(x,y,s=1,c='g',marker='s',linewidths=0)  #以绿色画散点图
axes[1].scatter(x,y,s=1,c=c,marker='s',linewidths=0)	#以不同颜色画散点图
for ax in axes:
    ax.axis("off")										#不显示子图的坐标系
plt.subplots_adjust(left=0,right=1,bottom=0,top=1,wspace=0,hspace=0)  #调整子图间距
plt.show()

Case 2 - 洛伦兹吸引子

数学名词：混沌数学、常微分方程

据说蝴蝶扇动翅膀这样一件小事，可能最终会引起对面半球的一场飓风。

——混沌理论

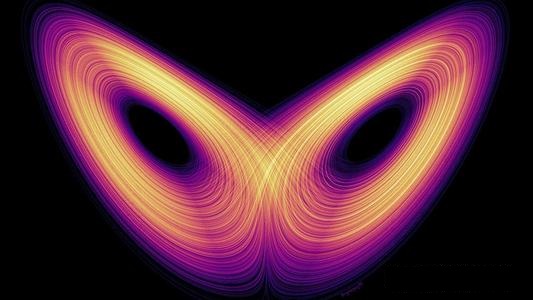
1544496822948

工作原理：气象学家Edward Lorenz建立的Lorenz吸引子是混沌理论的经典，它可由下述三个微分方程定义：
$$
\frac{dx}{dt}=\sigma(y-x), \quad \frac{dy}{dt}=x(\rho-z)-y,\quad \frac{dz}{dt}=xy-\beta z
$$
其中，σ, ρ, β为参数。这些方程定义了三维空间中的一个无质量点(x,y,z)的各轴坐标相对于时间的速度矢量。从某个坐标开始沿着速度矢量进行积分，可以计算出无质量点在三维空间中的运动轨迹。当参数为某些值时，轨迹出现混沌现象：微小的初值差别也会显著影响轨迹。

实例代码：常微分方程可用scipy模块的ode求解，但为降低解释的复杂度，我们使用“原始”的方法来进行求解。

#LorenzAttractor.py
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def lorenz(x, y, z, s=10, r=28, b=2.667):
    dt = 0.01							#t上的步长
    xOffset = s*(y - x)*dt
    yOffset = (x*(r-z) - y)*dt
    zOffset = (x*y - b*z)*dt
    return xOffset,yOffset,zOffset		#对应dx, dy, dz

stepCnt = 10000							#积分总步数
xs = [0 for i in range(stepCnt+1)]		#包括10001个元素的一维数组
ys = xs[:]                              #切片复制
zs = xs[:]
xs[0], ys[0], zs[0] = (0., 1., 1.05)	#初始化出发点坐标

for i in range(stepCnt):				#对时间积分
    xOffset,yOffset,zOffset = lorenz(xs[i], ys[i], zs[i])
    xs[i + 1] = xs[i] + xOffset
    ys[i + 1] = ys[i] + yOffset
    zs[i + 1] = zs[i] + zOffset

fig = plt.figure(figsize=(7,4))
ax = fig.gca(projection='3d')			#获取当前子图，指定三维模式

ax.plot(xs, ys, zs, lw=0.5)				#在当前子图中绘制吸引子曲线
ax.set_xlabel("X Axis")					#设置各轴标题
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title("Lorenz Attractor")		#设置子图标题

plt.show()

Case 3 - Mandelbrot Set

数学名词：分形数学、复平面

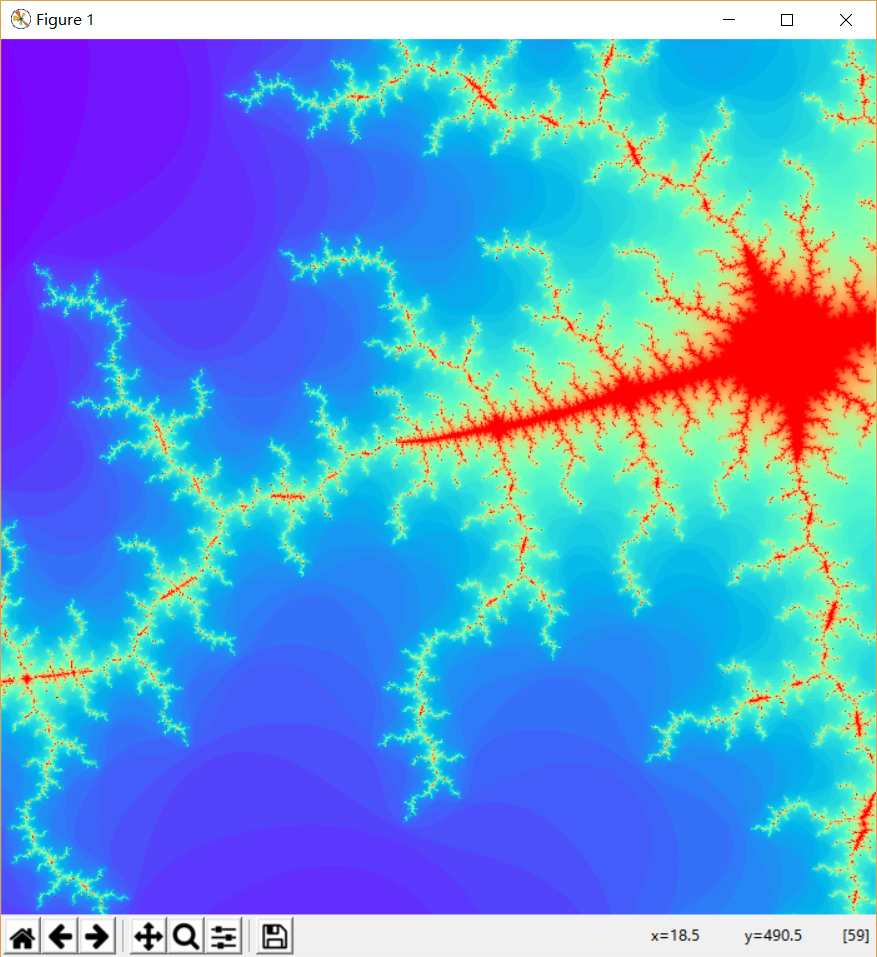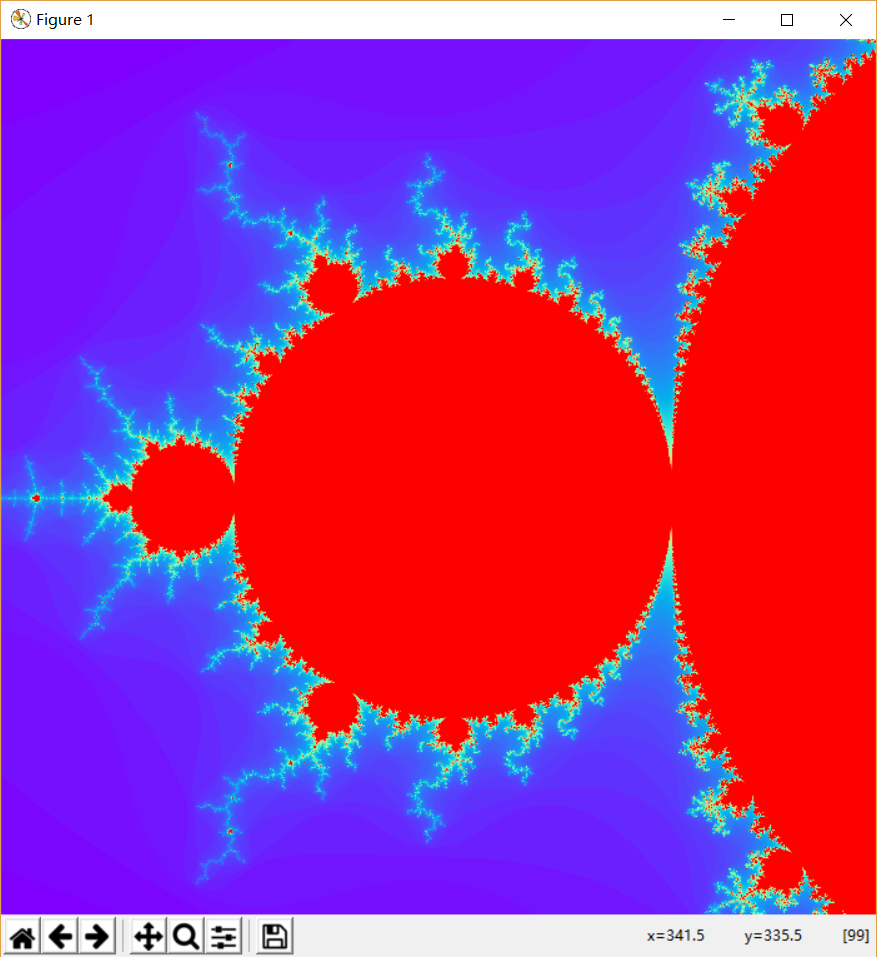
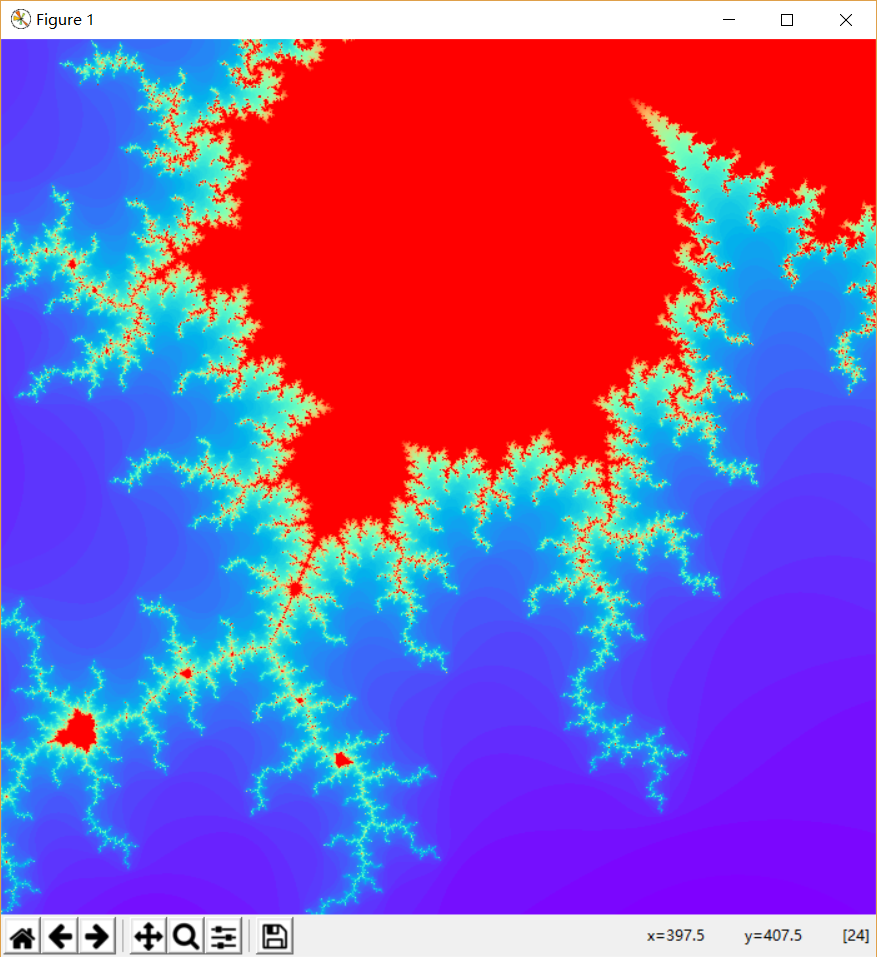
工作原理：Mandelbrot(曼德布洛特)集是在复平面上构成分形图案的点的集合。它可以用下述复二次多项式定义：
$$
f_{c}(z)=z^{2}+c
$$
这里的c = x + yi是一个复数，如果把实部x和虚部y视为复平面上的横纵坐标的话，那么c对应该复平面上的一个点。从z=0开始，反复应用上述二次多项式进行迭代计算，z值将不断变化，其或者延伸至无限大，或者停留在有限半径的圆内部。如果是后者，我们称参数c导致了不发散的迭代z序列，此时，c点属于Mandelbrot集合，否则不属于。对于复平面上的每一个离散坐标点，使用上述二次多项式计算其逃逸时间，并将逃逸时间映射成点的颜色，即得上述五光十色，具备无限细节的分形图象。

实例代码：这个… 稍稍有点长，略了。涉及numpy模块的使用，Cython代码的书写及编译。

Case 4 - 定积分求解

数学名词：定积分、极限

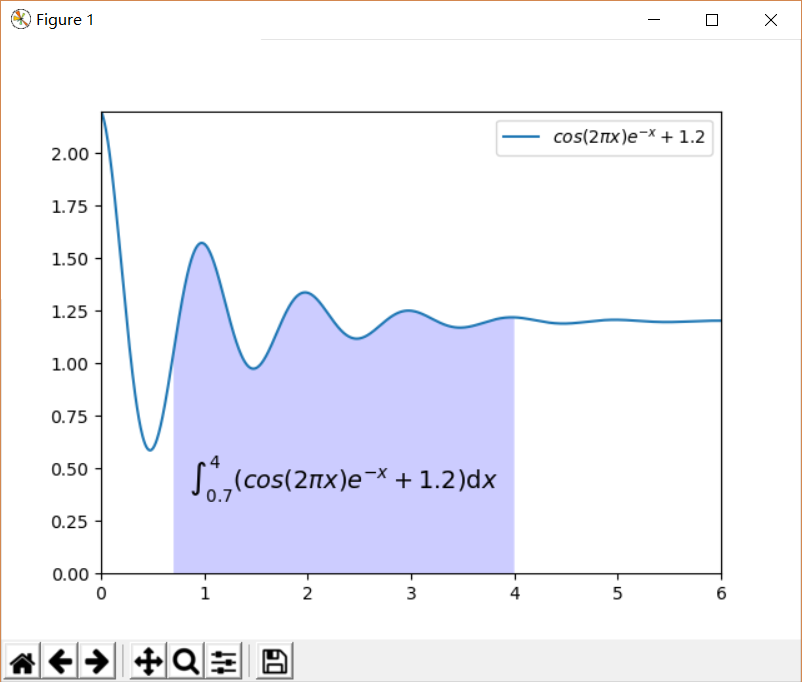
1545797416235

工作原理：这个就很常规了，就是使用矩形法把阴影部分分成很多很多的小矩形，对每个矩形求面积，再取和。
$$
\int_{0.7}^4(cos(2\pi x)e^{-x}+1.2)\mathrm{d}x
$$
实例代码：

#Integrate1.py
import numpy as np
from matplotlib import pyplot as plt

x = np.linspace(0,6,1000)
y = np.cos(2*np.pi*x)*np.exp(-x)+1.2

plt.axis([np.min(x),np.max(x),0,np.max(y)])           #坐标范围
plt.plot(x,y,label="$cos(2\pi x)e^{-x}+1.2$")      	  #画曲线，带图示
plt.fill_between(x,y1=y,y2=0,where=(x>=0.7)&(x<=4),   #填充积分区域
                 facecolor='blue',alpha=0.2)
plt.text(0.5*(0.7+4),0.4,r"$\int_{0.7}^4(cos(2\pi x)e^{-x}+1.2)\mathrm{d}x$",
         horizontalalignment='center',fontsize=14)    #增加说明文本
plt.legend()                                          #显示图示
plt.show()

#Area.py
import numpy as np

x = np.linspace(0.7,4.0,1000)
y = np.cos(2*np.pi*x)*np.exp(-x)+1.2
dx = x[1] - x[0]                        #每个矩形的宽度
fArea = np.sum(y*dx)                    #矩形宽*高，再求和
print("Integral area:",fArea)