除了祖冲之的割圆法和格雷戈里公式，借助于循环和随机数，我们还可以通过一种特别有趣的方法来估算圆周率。

版权声明

本文可以在互联网上自由转载，但必须：注明出处(作者：海洋饼干叔叔)并包含指向本页面的链接。

本文不可以以纸质出版为目的进行改编、摘抄。

  在历史的长河里，从古至今的数学家们尝试了无数种计算圆周率的方法。 其中，法国数学家布冯（1707年~1788年）和拉普拉斯（1749年~1827年）提出的方法比较有趣。

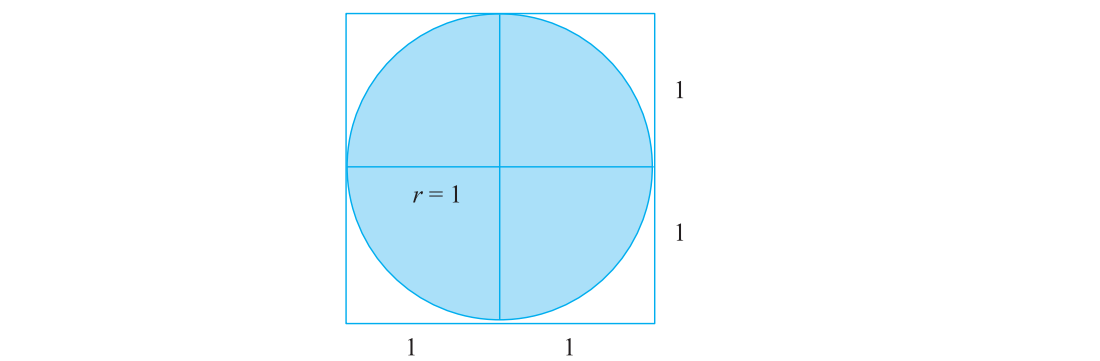
  在边长为2的正方形内有一个直径为2半径为1的内切圆。如图6-2所示。根据圆面积的计算公式，内切圆的面积 s = πr² ，由于r=1，所以π = 内切圆的面积。边长为2的正方形面积为4，那么在已知正方形的面积为4的情况下，如何求得内切圆的面积呢？ 布冯提出了投针的方法。假设10 000根针“均匀随机”地垂直落在正方形上，每根针在正方形上形成一个“投点”，那么落入圆内的投点数量与圆的面积正相关，即：

image-20221102104529385

简单推导，可得：

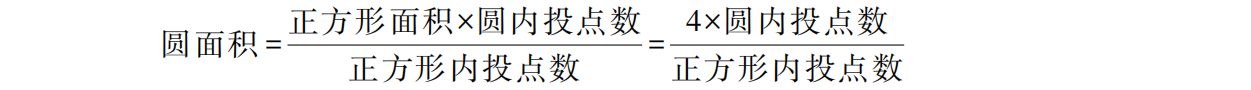
image-20221102104545743

  假设有8 000根针落在了圆内，其余的2000根落在了圆外。此时，内切圆面积 ≈ 4 × 8 000 / 10 000 = 4× 0.8 = 3.2，即圆周率π ≈ 3.2。

image-20221102104603446

  下述代码模拟了上述过程，即将数量众多的针投射到正方形，然后通过估算内切圆面积求得π。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//Project - FindPi
#include <iostream>
#include <cmath>
using namespace std;

int main()
{
    const int N = 10000;    //投点总数
    int nHits = 0;          //圆内投点数

    for (int i=0;i<N;i++){
        double x = 2.0*rand()/RAND_MAX - 1.0; //随机数取投点x坐标
        double y = 2.0*rand()/RAND_MAX - 1.0; //随机数取投点x坐标
        if (x*x + y*y <= 1.0)  //投点位于内切圆内
            nHits += 1;        //圆内投点数+1
    }

    double pi = 4.0*nHits/N;   //通过计算圆面积估算圆周率
    cout << "pi = " << pi;
    return 0;
}

上述程序的执行结果为：

1
pi = 3.1464

第8 ~ 9行：常量N代表投点总数，变量nHits表示落在圆内的投点数。

第11 ~ 16行：使用循环进行N次投点。

第12 ~ 13行：随机计算投点的x坐标和y坐标。rand()返回0 ~ RAND_MAX的随机整数，rand()/RAND_MAX的值域为0 ~ 1，将该值乘2再减1，即得取值范围为-1 ~ +1的随机数。理论上，rand()函数返回的随机数在值域内是“均匀”分布的。

注意： 整数(rand())/整数(RAND_MAX)的结果为整数，为了确保整个计算过程统一使用双精度浮点数进行计算，作者先用2.0*rand()，然后再除RAND_MAX，由于2.0是double类型的字面量，C++会将rand()返回的整数类型提升为double，再与2.0进行相乘…

第14行：计算投点距离圆心的距离，如果距离<=1.0，说明投点在圆内。注意，作者在这里没有使用sqrt()进行开方运算，由于圆的半径是1.0，此时的开方在数学上是可以省略的。由于开平方运算需要花费大量的CPU时间，这种处理很有价值。

第15行：如果投点在圆内，将nHits加1。

第18行：按前述公式估算圆的面积，也就是pi。注意，正方形的面积为4.0。

  为了更形象地向读者展示投点法估算圆周率的数学原理，我们还用Python中的绘图库matplotlib绘制了下述投针示意图：这些投针点“均匀”地投在了正方形内，多数落入圆内，少数落在圆外。

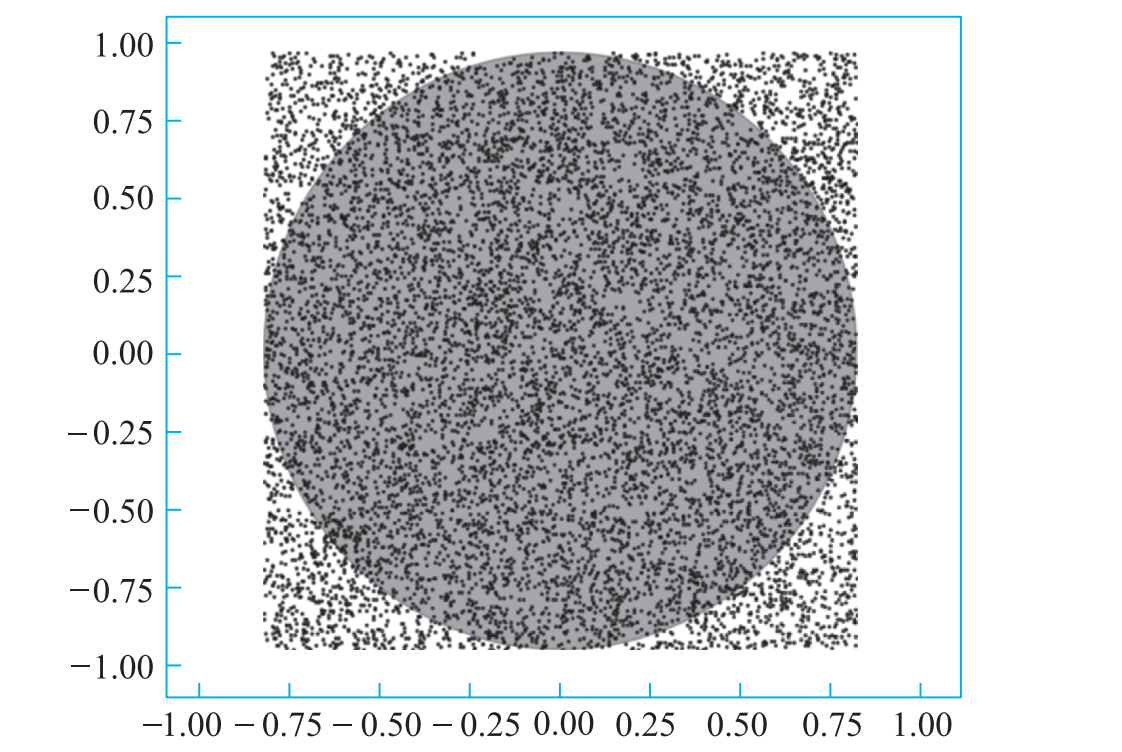
image-20221102104633742

  读者可能会觉得上述圆周率的估算值3.1464不够准确。请修改N值，增加投针数量，再试一试。理论上，N越大，结果越精确。


  C++